大平均は、次のようになります。
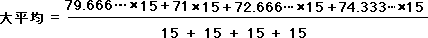
= 74.4166… = 74.42
| |
クリスピー |
普通 |
| 辛口 |
79.666… |
72.666… |
| 普通 |
71.00 |
74.333… |
次に、それぞれのズレを計算します。
今回の場合、データ数がそれぞれ同じですが、データ数が各々の条件で違う場合は、全条件に共通する「平均データ個数N」を計算しなければなりません。
例:下のようなデータ数の分析を行う場合、平均データ個数Nは、
| 要因A |
A1 |
A2 |
| 要因B |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
| データ数 |
14 |
10 |
13 |
17 |
12 |
15 |
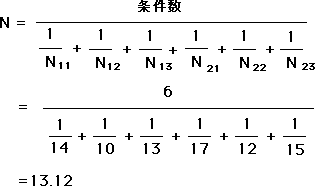
(Nの添字は条件番号)
になります。これ以後、この分析は各条件のデータ数がみな個数が等しいN=13.12であるとし、計算します。
1. A要因の平均のズレを計算する

A要因(クリスピーor普通)の平均のズレは、他の要因(ここでは要因B(辛口or普通))の効果をはずして計算する必要があります。
そこで、要因Aの条件内の平均と大平均とのズレを求め、データの個数倍(要因Bの種類数×全部の条件の平均データ個数)します。今の場合、要因Bが2種類あるので、データ数は2N(Nは全条件の平均データ個数=15)になります。
よって今回の式は、次のようになります。
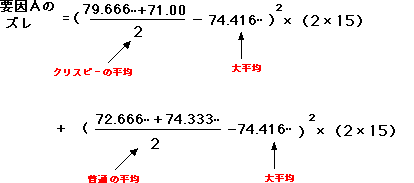
これを計算してください。
要因Aのズレは
2. B要因の平均のズレを計算する
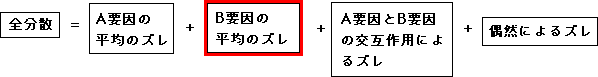
B要因(辛いor普通)の平均のズレは、今度は上とは逆に、要因A(クリスピーorノーマル)の効果をはずして計算する必要があります。
今の場合、要因Aが2種類あるので、データ数は2N(Nは全条件の平均データ個数=15)になります。
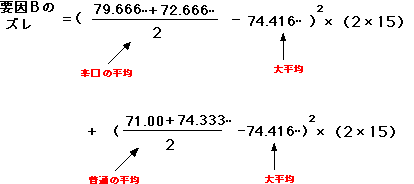
これを計算してください。
要因Bのズレは
3. A要因とB要因の交互作用によるズレを計算する

A要因とB要因の交互作用によるズレは、全条件の平均のズレを計算し、これからA要因とB要因のズレを引くことで求められます。それが、それぞれ単独では説明できない、A要因とB要因がお互いが影響しあってできたズレだと考えられます。
そこで、まず全条件の平均のズレを計算します。各条件の平均と大平均とのズレを計算し、データの個数倍して、足していきます。
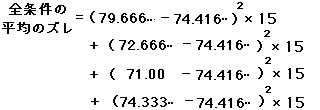
これから、A要因、B要因のズレを引きます。
交互作用によるズレ = 全条件の平均のズレ-A要因のズレ-B要因のズレ
A要因とB要因の交互作用によるズレを計算してください
A要因とB要因の交互作用によるズレは
4. 偶然の差によるズレを計算する
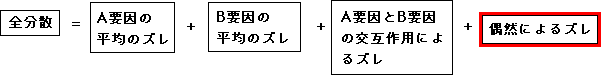
最後に、偶然の差によるズレを計算します。
偶然の差によるズレは、それぞれの標準偏差の二乗を合計し、データの個数をかけると簡単に求められます。
| 要因A |
クリスピー |
普通 |
| 要因B |
辛口 |
普通 |
辛口 |
普通 |
| データ数 |
15 |
15 |
15 |
15 |
| 標準偏差 |
7.6303… |
7.1180… |
7.4981… |
7.7172… |
今回の場合は、標準偏差が上のように求められているので、式は次のようになります。
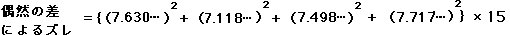
偶然の差によるズレを計算してください。
偶然の差によるズレは
終わったら次に進む