平均の差によるズレは
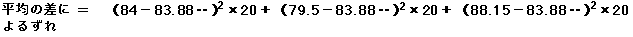
=748.6333… =748.63 になりました。
よって、今回の は、
は、
2494.18 = 1745.55 + 748.63 となります。
(2494.1833…) (748.6333…)
これから、ズレの原因はどこにあって、それが有意であるか、有意でないかを見ていきます。
そこで、検定を分かりやすくするため「表」を作ってみましょう。
<分散分析表>
この表の中に、今回の数値を埋めていきます。
(1)要因 とは? ----- データの分散を生じさせた原因 のこと
ですから、その下の欄にはデータの条件が入ります。今の場合だと
| 要因 |
平方和 |
自由度 |
平均平方 |
F比 |
| 平均の差 |
|
|
|
|
| 偶然の差 |
|
|
|
| 全体 |
|
|
が入ります。
(2)平方和 とは? ----- ズレの分散値の合計 のこと
よって、さきほど出したズレの値が入ります。
分散分析表には都合上、小数点第2位までの値を記入してありますが、計算過程では、そのままの値を用います。
| 要因 |
平方和 |
自由度 |
平均平方 |
F比 |
| 平均の差 |
748.63 |
|
|
|
| 偶然の差 |
1745.55 |
|
|
| 全体 |
2494.18 |
|
(3)自由度 とは? ----- ここでは要因ごとの固有の値をとらなければならない
ここでは、
平均の差の自由度 = 条件数 - 1
偶然の差の自由度 =(条件Aのデータ数-1)+(条件Bのデータ数-1)+・・・
全体の自由度 = データの総個数 - 1
今回の数値を当てはめると・・・
平均の差の自由度 = 3 - 1 = 2
偶然の差の自由度 =(20-1)+(20-1)+(20-1)= 57
全体の自由度 = 60 - 1= 59
| 要因 |
平方和 |
自由度 |
平均平方 |
F比 |
| 平均の差 |
748.63 |
2 |
|
|
| 偶然の差 |
1745.55 |
57 |
|
| 全体 |
2494.18 |
59 |
(4)平均平方 とは? ------ 自由度一個分に平均した平方和 のこと
自由度の大きい要因は平方和も大きくなるので、要因の平方和を比べるときに、
そのままでは公平な比較にならなりません。そこで、自由度一個分の値に換算する必要があるのです。
だからここには、
748.6333… ÷ 2 = 374.3166… となります。表では、374.32とします。
1745.55 ÷ 57 = 30.6236… が入ります。表では、30.62とします。
| 要因 |
平方和 |
自由度 |
平均平方 |
F比 |
| 平均の差 |
748.63 |
2 |
374.32 |
|
| 偶然の差 |
1745.55 |
57 |
30.62 |
| 全体 |
2494.18 |
59 |
(5)F比 とは? ----- 平均の差によるズレが偶然の差によるズレの何倍になるかを示したもの
今回の場合、 374.3166… ÷ 30.6236… の計算になります。
| 要因 |
平方和 |
自由度 |
平均平方 |
F比 |
| 平均の差 |
748.63 |
2 |
374.32 |
|
| 偶然の差 |
1745.55 |
57 |
30.62 |
| 全体 |
2494.18 |
59 |
このF比がかなり大きければ、偶然の差ではなく、平均の差によって各条件の差が生じたと認めてもよい、ということになります。
では、F比を出してみてください。
F比は になる。
終わったら答えを見る