ぞれでは、偶然のズレの細かいズレを求めてみましょう。
偶然のズレは次の4つに分解されます。

1、個人差によって生じる分散を計算する
個人差は、被験者と被験者の差異です。
個人差には、それぞれの被験者の合計を用いるため、それぞれの合計を求めます。それが下の表になります。
合計のところに、それぞれの番号の人がだした得点の合計を載せました。
| |
箱 |
紙 |
合計 |
| つくりおき |
注文 |
つくりおき |
注文 |
| 1 |
65 |
70 |
50 |
60 |
245 |
| 2 |
75 |
80 |
55 |
65 |
275 |
| 3 |
70 |
75 |
70 |
75 |
290 |
| 4 |
75 |
75 |
75 |
80 |
305 |
| 5 |
90 |
95 |
80 |
90 |
355 |
| 6 |
80 |
80 |
85 |
80 |
325 |
| 7 |
65 |
75 |
65 |
80 |
285 |
| 8 |
50 |
55 |
55 |
55 |
215 |
| 9 |
55 |
50 |
55 |
60 |
220 |
| 10 |
80 |
85 |
75 |
82 |
322 |
| 11 |
90 |
80 |
80 |
80 |
330 |
| 12 |
70 |
70 |
75 |
70 |
285 |
| 13 |
75 |
75 |
70 |
90 |
310 |
| 14 |
80 |
80 |
65 |
70 |
295 |
| 15 |
75 |
60 |
55 |
60 |
250 |
合計が出たところで、修正項を求めます。修正項とは、そのデータにおける全体のばらつきを合計で示したものです。
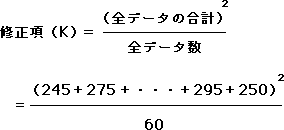
そして、個人差を計算します。次のように計算します。

今の場合、「一人あたりのデータ数」とは、一人が4個のハンバーガーの点数を出しているのでデータ数は 4 になります。
計算して個人差を求めて下さい。
2、A要因に対する(偶然の)ズレを求める
ここからは、被験者個人内のズレになります。
まず、被験者個人が要因A(ここでは箱or紙)に対して生じるズレを計算します。
そこで、次のような補助表を作ります。被験者ひとり一人要因Aのみの合計を計算しておきます。
| |
箱 |
紙 |
| 1 |
65+70=135 |
50+60=110 |
| 2 |
75+80=155 |
55+65=120 |
| 3 |
・
・
・
・
・
・
・
・
・ |
・
・
・
・
・
・
・
・
・ |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
75+60=135 |
55+60=115 |
そして、次の式で、要因Aにおける偶然のズレを求めます。

「一マスあたりのデータ数」とは、上の補助表の一マスにあるデータの数です。例えば「箱」の1番目のマスには65と70という2つのデータがあるので、データ数は 2 になります。
計算してA要因に対する(偶然の)ズレを求めて下さい。
2、B要因に対する(偶然の)ズレを求める
被験者個人が要因B(ここではつくりおきor注文)に対して生じるズレを計算します。
次のような補助表を作ります。被験者一人一人要因Bのみの合計を計算しておきます。
| |
つくりおき |
注文 |
| 1 |
65+50=115 |
70+60=130 |
| 2 |
75+55=130 |
80+65=145 |
| 3 |
・
・
・
・
・
・
・
・
・ |
・
・
・
・
・
・
・
・
・ |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
75+55=130 |
60+60=120 |
そして、次の式で、要因Bにおける偶然のズレを求めます。

「一マスあたりのデータ数」とは、要因Aにおける偶然のズレを求めるときと同様に、上の補助表の一マスにあるデータの数です。例えば「つくりおき」の1番目のマスには65と50という2つのデータがあるので、データ数は 2 になります。
計算してB要因に対する(偶然の)ズレを求めて下さい。
3、交互作用に対する(偶然の)ズレを求める
交互作用以外の値はでそろったので、偶然によるズレから、他の値を引けば、交互作用のズレは求まります。

計算して交互作用に対する(偶然の)ズレを求めて下さい。
終わったら答えをみる