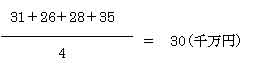←講義のツボメニューへ
統合情報システム学
【2002.5.21】【第11回】
季節変動
季節変動は、1年を周期とした変動であるから、
月あるいは四半期ごとに観察された時系列の場合に問題となる。
季節変動のほかにも1ヶ月あるいは1週間を周期とするごく短期の規則的な変動もある。
しかし、これらは季節変動と同じように分析できる。
| 年次 | 四半期 | 売上高(千万円) |
|---|
| 1982年 | 1 | 31 |
| | 2 | 26 |
| | 3 | 28 |
| | 4 | 35 |
| 1983年 | 1 | 33 |
| | 2 | 28 |
| | 3 | 31 |
| | 4 | 37 |
| 1984年 | 1 | 34 |
| | 2 | 30 |
| | 3 | 33 |
| | 4 | 43 |
右のような場合、移動平均法で季節変動を分析する。
まず、売上高から1年間の移動平均値を計算する。
たとえば、1982年の第1四半期から第4四半期までの1年間の移動平均値は
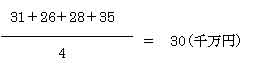
で計算することができる。
この結果は第2四半期と第3四半期の間に記入する。
以下同様に計算、記入していく。
次に今計算した移動平均値2つの平均をとる。つまり、
第2四半期と第3四半期の間に記入された移動平均値と
第3四半期と第4四半期の間に記入された移動平均値の平均をとる。
その計算結果をその2つの間に記入する
すると、第3四半期の直線状に記入されることになる。
以上の全ての結果を表にすると以下のようになる
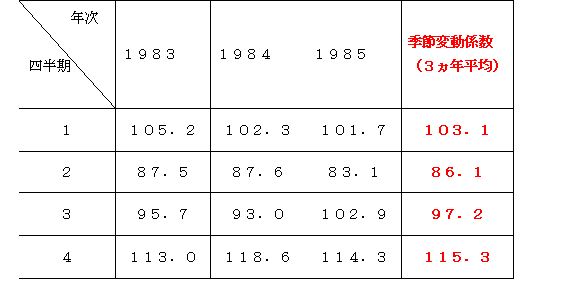
移動平均法による季節変動の計算
また、上記リンク先にある表の(4)列の比率を四半期ごとに平均する。
この平均値を季節変動係数という。