←講義のツボメニューへ
統合情報システム学
【2002.5.14】【第9回】
回帰分析と需要予測
傾向変動の分析
| 年次 | 売上高 |
|---|
| 1977年 | 104 |
| 1978年 | 124 |
| 1979年 | 146 |
| 1980年 | 152 |
| 1981年 | 177 |
| 1982年 | 196 |
| 1983年 | 240 |
| 1984年 | 304 |
| 1985年 | 352 |
| 1986年 | 376 |
右の表はある企業の売上高の数字である
この系列には、一定の傾向があることが見て取れると思う
年を追うごとに売上高が上昇している
これを上向きの傾向変動があるという
時系列のグラフで、統計文字を表す点、またはその近くを通って変動の基本的傾向を示すと考えられるような線を傾向線という。
傾向線を求める方法には目測法・移動平均法・最小二乗法などがある。
目測法
目測法・・・グラフの点を見て目分量で全体の傾向を表す
つまり、大体の予測を立てて傾向線を書いてみる手法
書き方は簡単だが、どうやっても正確性は出ないので
正式な傾向線を求める場合はあまり使用されない
| 年次 | 売上高 | 移動平均値 |
|---|
| 1977年 | 104 | − |
| 1978年 | 124 | − |
| 1979年 | 146 | 140.6 |
| 1980年 | 152 | 159.0 |
| 1981年 | 177 | 182.2 |
| 1982年 | 196 | 213.8 |
| 1983年 | 240 | 253.8 |
| 1984年 | 304 | 293.6 |
| 1985年 | 352 | − |
| 1986年 | 376 | − |
移動平均法
移動平均法・・・与えられた時系列の各項について、その項を中心とする前後一定期間の項の平均値を計算し、その平均値を連結して傾向線を示す方法。
最初に取り上げた表の移動平均値は右表のようになります
この1979年の移動平均値は以下の計算式で求められます
(104+124+146+152+177)÷5=140.6(百万円)
1980年の移動平均値を求めたい場合は1年ずらして計算する
(124+146+152+177+196)÷5=159.0(百万円)
最小二乗法
まず、N年間の時系列データを
Y1,Y2,Y3,・・・・,YN
とし、その傾向値を
Y'1,Y'2,Y'3,・・・・,Y'N,
としたとき、傾向変動が直線で表されるということは
Y't=a+bt
と書き表せるということである。
ここではaとbは定数である。
個人的にはy=ax+bの方が高校時代より慣れ親しんでいるので
こちらの式の方が覚えやすいと思う
さて、この定数aとbを如何にして求めるかだが、時系列を利用して以下の公式で求める
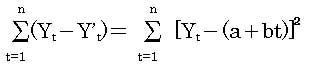
この式が最も小さくなる値がaとbの定数となる
そのために以下の連立方程式を解く
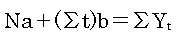
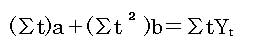
この2つの方程式のことを正規方程式という。