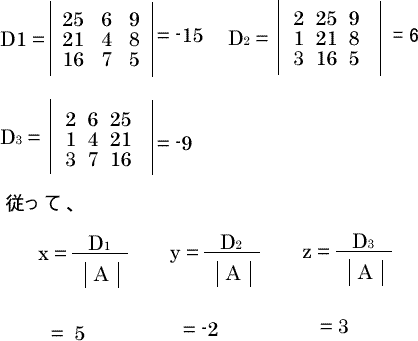行列式

【日付：5月7日】【連載回数3回】

行列式の定義
ｎ次元の正方行列

に対して、Aの行列式は

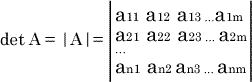
と定義される。

※行列と行列式→行列の大きさをあらわしたものが行列式

行列式の基本性質

1. 2つの列を交換すると、行列式の値は符号だけ変える。
2. ある列をt倍すると、行列式の値もt倍になる。
3. ある列が2つのベクトルの和になっている行列式は、それぞれのベクトルをその列とする2つの行列式の和に等しくなる。
4. ある列のt倍をほかの列に加えても行列式の値は変わらない。

余因子
行列A(i,j)をｎ(n<2)次の正方行列にするとき、行列Aの行i、列jを削ってできた(n-1)次の行列式をMijであらわし、
Aの小行列式という。更に、aijの余因子というものを次のように定義する。
Aij = (-1)_i+jM_ij

クラメルの公式
例題

2x+6y+9z=25
x+4y+8z=21	を、クラメルの公式によって解け。
3x+7y+5z=16