行列のランク

【日付：５月２１日】【連載回数3回】

1.ベクトルの一次独立・一次従属

同一次元のk個のベクトルa1,a2...,akについて、 ｔ1a1 + t2a2 + ・・・ + tkak = 0 が成立するが、 t1 = ... = tk = 0の場合だけのとき、a1, ... , ak は一次独立、 t1 = ... = tk = 0以外にもあるとき、a1 , .. ak 　は一次従属 であるという。

かみくだくと・・・

まず、t1a1 + t2a2 + ・・・ + tkak = 0というのがあって、この式をひとつの方程式に見立てる。

なじみやすくすると、こんな感じになります。
ax + by + cz = 0…�@
ここで、a,b,cがそれぞれt1,t2,t3に、x,y,zがそれぞれa1,a2,a3になります。
�@の方程式ではa,b,cは定数です。たとえば、3x + 4y + 8z = 0のように。
ここで、方程式の解が0の場合だけ一次独立といって、
０以外にもあれば一次従属といいます。

2.行列の階数
行列の一字独立な列ベクトルの最大個数を行列Aのランクと呼び、rankAなどと記す。たとえば、

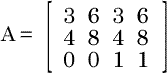
の４個のベクトルを

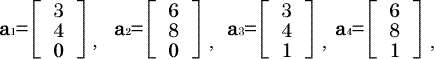
とおけば、a1,a3は一時独立という２個のベクトルa1,a3が確かに存在する。しかし、よく見ると、
a2 = 2a1, a4 = a1 + a3
だから、三個以上のれつベクトルをとると必ず一時従属になってしまうので、
rank A = 2
ということになる。

3.階段行列

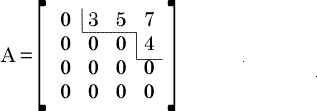
上記のように左側に連続して並ぶ０の個数が増えるような行列を階段行列とよぶ。このとき、各行の０でない最初の成分a1k1,…,
arkrの個数rがこの階段行列の階数である。