ハードウェア基礎
2002年度版テキスト
2.電気回路
2.1.電気回路とは
図2.1に示すように、電流が還流するループ状の一連の配線を電気回路という。
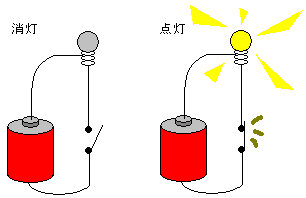 図2.1 電気回路
図2.1 電気回路
この電気回路では、電池が内部の化学エネルギーによってその両端にある電位差を発生し、
回路に電力を流す力(起電力)を持っている。電流は電池の+端子から出発して、ランプ
を経由して−(マイナス)端子へ還流する。途中の電線は良導体なので、
エネルギー消費は発生しないが、ランプは熱エネルギーと光エネルギーを消費する
抵抗素子である。電気回路はこのように必ず閉じたループとなっている。さもないと
電流の還流が完結せず、よって電流が流れない。途中にあるスイッチをオフにすると、
ループが切れるので電流は流れず、したがってランプも点灯しない。
2.2.オームの法則
2.1図のような電気回路で、電流、電圧や抵抗の代償関係を種々実験した結果、
オームは次の関係を発見した。
電流 ∝ 電圧 / 抵抗(2.1式)
電流の単位をアンペア(A)、電圧の単位をボルト(V)、抵抗の単位をオーム(Ω)
で表現することとし、これらの単位を2.1式に当てはめると、ちょうど区切りよく
2.2式のようになるように単位が決められている。
1A = 1V / 1Ω(2.2式)
1Aという電流は、かなり大きい量の電流であり、家電品では大体この程度の電流になる。
5A = 100V / 20Ω(中型テレビ)
電子回路では、電流の量はほぼ1/1000の程度である。
1mA = 5V / 5kΩ(1個のIC)
2.3.抵抗のつなぎ方
円筒形の物体があり、その筒の軸方向に電流を流すとき、この物体の電気抵抗値Rは、
1.筒の長さに比例する R ∝ L(2.3式)
2.筒の断面積(円形)に反比例する R ∝ L / S(2.4式)
となる。
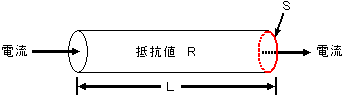 図2.2 抵抗の性質
図2.2 抵抗の性質
2.3式、2.4式ををあわせて一つの関係式に書くと、
R ∝ L / S(2.5式)
となる。このことから容易に2個の抵抗を2.3図(a)および2.3図(b)のように接続すると、
2個の合計の抵抗値は次のようになることがわかる。
 図2.3(a)
図2.3(a)
R2個を直列接続すると合計の抵抗値は
2Rとなる。
(なぜならば合計の長さが2倍となる。合計抵抗値は長さに比例する。)
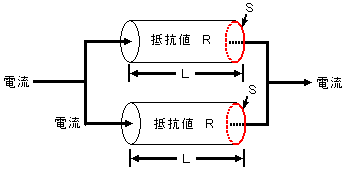 図2.3(b)
図2.3(b)
R2個を並列接続すると、合計の抵抗値は
R/2となる。
(なぜならば合計の断面積が2倍になる。合計抵抗値は断面積に反比例する。)
抵抗の個数を2個以上に増やした場合にも同様の関係が成り立つ。(長さと断面積に置き換えて
考えればよい。)実際の直列接続と並列接続の状況を3個のランプの例で示す。
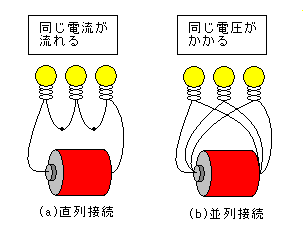 図2.4 3個のランプ(抵抗)の直列接続と並列接続
図2.4 3個のランプ(抵抗)の直列接続と並列接続
図2.4を電気回路図として、電気回路記号を使って描くと、図2,5、図2,6のようになる。
まず直列接続の2,5図のばあを考える居。3個のランプが同一ならば、3個の抵抗値は等しい。
仮にその値をR1(=R2=R3)とすると、3個あわせた全体の抵抗値Rは上記より
R=3R1となる。もしR1とR2とR3がそれぞれ等しくなければ、
R=R1+R2+R3 (式2.6)
となる。(個々の抵抗の長さが違っても、その合計の長さに比例することには変わり無いため)
したがってこれら3個の直列抵抗を還流する電流Iは式(2.7)で計算できる。
I=E/R = E/(R1+R2+R3) (式2.7)
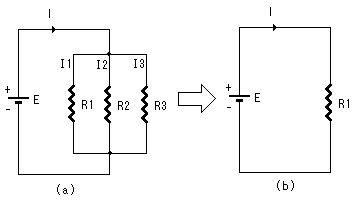 図2.5 直列接続
図2.5 直列接続
並列接続の場合は、3個の抵抗値が等しくR1ならば全体の抵抗値Rは R=R1/3 となる。
もしそれぞれR1,R2,R3ならば、
R1/(R1の断面積+R2の断面積+R3の断面積)
=1/(1/R1+1/R2+1/R3) (式2.8)
となる。こうなることは2.6図において、I1=E/R1、I2=E/R2、I3=1/R3から導く。
すなわち、全体の電流Iは、3個の抵抗それぞれにながれる電流の合計値だから、
I=I1+I2+I3
=E/R1+E/R2+E/R3
=E(1/R1+1/R2+1/R3) (式2.9)
となる。ここで、(2.9)式の右辺のE( )の括弧の部分を無理やり分母におろして、E/□の形に
したい。そうするとその□が全体の抵抗値を表すことになる。(電流=電圧/抵抗の形に無理やりそろえる。)
すなわち、
I=E/1/(1/R1+1/R2+1/R3)=E/R (式2.10)
この(2.10)式は、(2.8)式を別形式で表しているものである。
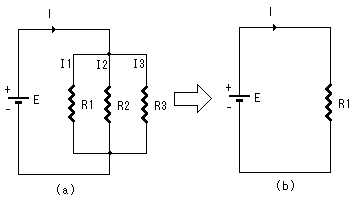 図2.6 並列接続
図2.6 並列接続
2.4.例外的に流れる電流(1)
閉じたループ回路が形成されていないのに電流が流れることが例外的にある。その一つは放電である。
放電は熱エネルギーや摩擦エネルギーで発生した静電気が原因となる。静電気発生の源のエネルギーがなくなると、
発生したプラスとマイナスの静電気は互いの引力によって再結合して元の中立状態へ戻ろうとする。しかし帯電物質
は絶縁体の場合が多いので、静電気(電子)は移動できずに帯電したままになる。そこへ何らかの別要因によって
帯電物が運動したり、中間に良導体が割り込んだりすると、再結合が助けられ放電が起こる。
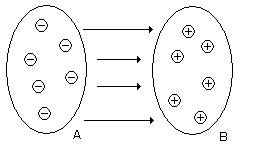 図2.7 静電気の放電
図2.7 静電気の放電
この場合、電流は2.7図のB点からA点へ流れたこととなり、閉ループを還流する形にはなっていない。
この現象は一瞬にして終わる過渡現象(Transiest Phenomena)である。他方、電源をもつ閉ループ回路を
還流するのは、定常的に流れる電流である。
1.5.例外的に流れる電流(2)
大きなアンテナを空中に立てて、その根元に直列に豆ランプをつなぐと、豆ランプが僅かに点灯する。
これはアンテナが空中を伝わってきた電磁波を受け、アンテナに小さな起電力が生じたためである。
この場合の起電力は電磁波の周波数(ヘルツ)と同じ周波数の興隆期電力であり、ランプに流れる
電流も、それに対応した交流電流である。これは過渡現象の連続ともみなしうる。
この場合も図2.8から明らかなように閉ループ回路ではないが、ある種の電流が流れる結果となる。
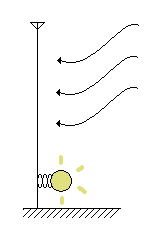 図2.8 アンテナによるランプ点灯
図2.8 アンテナによるランプ点灯
2.6.オームの法則で扱う直流回路
上記の2つの冷害はいずれも定常的な直流(流れる方向が変化しない)ではない。一方オームの
法則は、定常的な直流回路を対象としている。コンピュータやデジタル電子回路では、通常は
定常的な直流回路で構成される。(例外:携帯電話の受信発信部分)したがって我々の主たる
対象は定常的な直流回路であり、オームの法則(もっとも基礎的で簡単な法則である。)さえ
りかいしておればほとんど足りる。
以下、直流回路をオームの法則を使っていろいろ検討する時のポイントをあげる。
(1)オームの時代はまだ電子の存在が知られていなかった。しかし初歩的な電池やメーターを
使って実験を行い、電圧、電流、抵抗などの名称や記号や極性(どちらをプラスと呼ぶか)を
決めた。その後、実はマイナス電気量をもった電子が移動する事実がわかったので、オームの
考えた電流回路を考えるときは、電子の動く方向とは逆であることが判った。しかしあくまで
オームの法則をつかって回路を考えるときは、電子の方向のことは忘れて「高電位から低電位
へ(プラス量の)電流が流れる」との認識で分析をすすめてなんら問題は生じない。「低電位
から高電位へ電流が流れる」ことは絶対にありえない。
(2)地球(地面)は、砂粒や岩盤が主体であるかに思われるので、電気抵抗としては絶縁体
であるかに思われる。しかし実際は地球は良導体なのである。水や鉱物を含んでいること、
断面積が圧倒的に大なること、による。
(3)定常的な直流回路での電流は、必ず起電力を持った電源のプラス端子から出発して、
マイナス端子へ還流して戻る。どこか途中で消滅したり、途中から湧き出したりはしない。
逆にいうと、定常的な直流回路は必ずループ状に閉じている。さもないと回路をなしている
とはいえない。
(4)オームの法則は回路全体に対しても、回路の一部に対しても同じように成立する。
すなわち、回路全体において
電流全体 = 電圧全体 / 抵抗全体
であると共に、ある一部分に着目したとき、その着目部分において次の式が成立する。
電流部分 = 電圧部分 / 抵抗部分
(5)オームの法則の左辺、右辺を変形して
電流 × 抵抗 = 電圧
のスタイルにして使うことも多い。また、抵抗を複数個並列にしたときの全体の抵抗値を算出
するのは、分数計算の繰り返しになって面倒だが、実際にはそういう必要はあまり発生しない。
語句単純な計算のみで実用的な用は足りる。
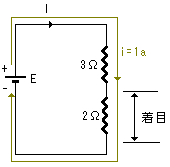
|
電流全体 = 電圧全体 / 抵抗全体
=5V/3Ω+2Ω=1A
着目部分の電圧=電流部分×抵抗部分
=1A×2Ω=2V
|
図2.9 オームの法則の部分回路への適用
(6)電位は本来は相対的なもので、比較する回路ポイントの間での高い低いの問題である。しかし
絶対的な電位ゼロの基準があることが、離れた地点を通信回路でつなぐ場合には必要となってくる。
この離れた場所においても容易に接続することが出来るからである。地球に電気的に接続することを
「接地する」または「アースする」という。実際には水道管に接続すると良い設置になる。
ある2点が接地することは、その2点を地球を通して接続したことにもなる。
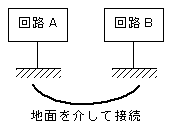 図2.10 2点での接地
図2.10 2点での接地










