偶然によるズレは、つぎのとおりになりました。
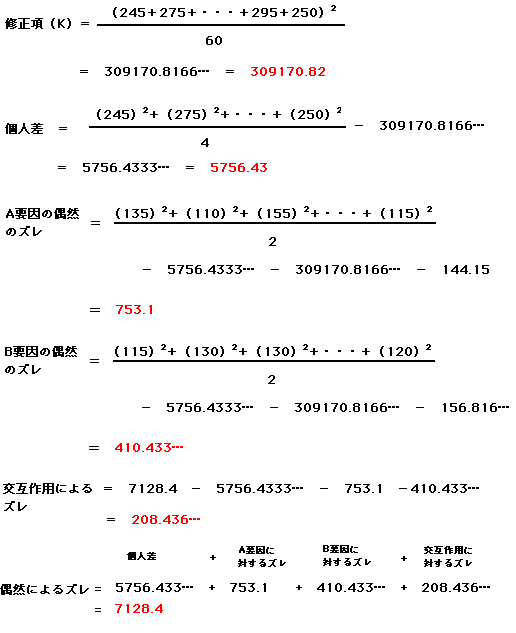
ズレがでそろったところで分散分析表を作成します。
今回の分析表は次のようになる。
要因 |
平方和 |
自由度 |
平均平方 |
F比 |
個人差(S) |
5756.43 |
|
|
要因A
S×A(要因Aの偶然のズレ) |
144.15
753.1 |
|
|
|
|
要因B
S×B(要因Bの偶然のズレ) |
156.82
410.43 |
|
|
|
|
A×B(交互作用)
S×A×B(偶然のズレ) |
99.82
208.44 |
|
|
|
| 全体 |
|
59 |
|
|
個人差はSで示し、Sのからんだ記号はすべてそれの被験者内の偶然のズレを示します。それぞれのF比もそれぞれの偶然のズレが分母になる。例えば、主効果である要因AのF比の分母は、要因Aの偶然のズレの値になります。
それぞれの自由度は次のとおり。
個人差----データ個数−1
要因A----要因A内の条件数−1
S×A----(個人差の自由度)×(要因Aの自由度)
要因B----要因B内の条件個数−1
S×B----(個人差の自由度)×(要因Bの自由度)
A×B---(要因Aの自由度)×(要因Bの自由度)
S×A×B----(個人差の自由度)×(交互作用の自由度)
それでは、表を完成させるために次の値をそれぞれ求めて下さい。
個人差
自由度
平均平方
要因A
自由度
平均平方
F比
S×A(要因Aの偶然のズレ)
自由度
平均平方
要因B
自由度
平均平方
F比
S×B(要因Bの偶然のズレ)
自由度
平均平方
A×B
自由度
平均平方
F比
S×A×B
自由度
平均平方
終わったら答えをみる